SEU程序设计复习01:基础语法
本学期涉及内容:
- 第二章:C++程序入门、输入输出和运算符
- 第三章:类、对象、字符串
- 第四章:控制语句、赋值、自增、自减
- 第五章:控制语句和逻辑运算符
- 第六章:函数和递归入门
- 第七章:类模版array和vector、异常捕捉(没学)
- 第八章:指针
第一章省流版:

欢迎进入C++的世界! C++功能很多。 计算机由各种基本单元组成。(不知道会不会考,但是反正是开卷的也无所谓了) 计算机有各种各样的编程语言。
面向对象
- 小汽车:对象
- 小汽车会跑:成员函数
- 小汽车蓝图:类
- 由蓝图制造小汽车:实例化、重用
- 踩踏板:成员函数调用
- 小汽车速度:属性、数据成员
- 驾驶员无需知道汽车工作原理:封装
- 由一般性的汽车细化设计得到敞篷车:继承
- 无论什么车都可以用方向盘控制:多态
各种内容总结
直接从书上复制内容太无聊了,所以后面的内容可能和书本章节并不对应,主打一个随心所欲。
良好的编程习惯

main函数
每个C++程序都要有,表示程序运行的入口。除非你要做并行计算,不管你的程序文件结构有多复杂,机器永远是像读纸带八音盒那样一条一条读你的程序。所以需要有一个函数作为入口是理所当然的,就像纸带必须要有个一端接入八音盒(我们不考虑某种环形或者莫比乌斯环形的纸带)。
一个简单的不能再简单的程序:
#include <iostream>
int main(int argc, char *argv[]) {
std::cout << "Helloworld!!" << std::endl;
return 0;
}
语句要用英文键盘的分号结尾。
你可以在开头使用using namespace std;来在后续写代码过程中省略std::的书写,但是一般认为这样做是可能带来不好后果的(比如假如你自己定义了某个函数名字恰好和std下的某个函数重合了,程序就会开始打架)。所以如果追求更好的程序质量,最好不要省略std::。
多个语句输出在一行:
int main(int argc, char *argv[]) {
std::cout << "Welcome to";
std::cout << "C++" << std::endl;
return 0;
}
感觉这个地方太简单了,我们稍微略过一些内容。
以下解答一些术语上的误区和一些我个人没那么有把握熟练掌握的东西:
什么是关键字?什么是标识符?
关键字就是程序语言自己定义的具有特定语义的单词,比如int表示整型,if表示条件判断,标识符则是程序员自己定义的,比如随便一个变量int thisIsARandomNumble = 1,没有人会把一个变量命名为if或者int(比如某人写int int = 1)。
using的用法
一个最简单的用法:引用整个命名空间:
using namespace std;
这样做是合法的,但是可能导致名字冲突,并降低代码可读性。一般不推荐省这一点代码量。
与之相比,只引入某个函数名是更加推荐的写法,可以更加灵活的避免命名冲突的同时加快写代码的速度。
using std::cout;
using std::endl;
// 表示后面的代码中不用写std::cout或者std::endl,直接写cout或者endl即可。
但是using的用法不止于此。比如如果你要处理一个比较大的数字,你可能需要用到容量比int更大的数据类型,一般的考虑对象就是long long,因为它的大小在各种环境下是固定的64个bit。但是,long long写起来太长了,这时候你就可以写using ll = long long;来给long long起个别名。
#include <iomanip>
#include <iostream>
using ll = long long;
const int n = 60;
int main(int argc, char *argv[]) {
ll temp = 1;
for (int i = 0; i < n; i++) {
temp <<= 1;
}
int counter = 0;
while (temp > 0) {
std::cout << temp << std::setw(4) << counter << std::endl;
counter++;
temp /= 2;
}
return 0;
}
这段代码的功能是计算了2的60次方,随后一直除2直到为0,记录其中的计算次数,证明一开始算出来的确实是2的60次方。输出结果如下:
1152921504606846976 0
576460752303423488 1
288230376151711744 2
144115188075855872 3
72057594037927936 4
36028797018963968 5
18014398509481984 6
9007199254740992 7
4503599627370496 8
2251799813685248 9
1125899906842624 10
562949953421312 11
281474976710656 12
140737488355328 13
70368744177664 14
35184372088832 15
17592186044416 16
8796093022208 17
4398046511104 18
2199023255552 19
1099511627776 20
549755813888 21
274877906944 22
137438953472 23
68719476736 24
34359738368 25
17179869184 26
8589934592 27
4294967296 28
2147483648 29
1073741824 30
536870912 31
268435456 32
134217728 33
67108864 34
33554432 35
16777216 36
8388608 37
4194304 38
2097152 39
1048576 40
524288 41
262144 42
131072 43
65536 44
32768 45
16384 46
8192 47
4096 48
2048 49
1024 50
512 51
256 52
128 53
64 54
32 55
16 56
8 57
4 58
2 59
1 60
但是如果我们开头不写using ll = long long;,而是写using ll = int;,程序就不会有任何输出(或者某些环境下会报错),原因是数据溢出了。
随机数生成
在cpp中有很多种方式可以用来生成随机数。其中,最省事的方法是直接使用<cstdlib>提供的rand()函数。这是一种从C语言时代遗留下来的老古董,应该说正经写cpp代码的时候不应该再使用这个函数了,但是不得不说在做一些小功能的时候这种写法非常方便。
#include <cstdlib>
#include <iostream>
int main(int argc, char *argv[]) {
while (true) {
int i = rand();
std::cout << i << std::endl;
bool state;
std::cin >> state;
if (state)
break;
}
return 0;
}
以上例子中,程序会一直生成一个随机数直到你输入1或者某个表示true的文本。某次输出如下:
1804289383
0
846930886
0
1681692777
0
1714636915
0
1957747793
0
424238335
1
看起来确实挺随机的,但是这样做有一个很大的问题:每次运行程序输出的随机数都一样。原因就在于其实rand()函数实现随机数的方式非常的蠢,蠢到你可以自己手算。rand()函数通常的实现方式如下:
int rand(void) {
next = next * A + C;
return (next / D) % M;
}
其中next是一个静态全局变量。你很容易发现:rand()的实现方式其实就是加减乘除。毫不夸张的说,你可以随便拉一个小学生过来给他一个初始值,让他帮你计算随机数。但是之所以这样做仍然得到推广,就在于它的实现效果比意料中的其实要好。
一个常见的参数如下:
A = 1103515245
C = 12345
M = 2^31
假如你随便告诉小学生一个初始值,让他帮你按照前面的算法一步步计算数值,虽然每一步都完全确定,但是对于一个不知道计算算法也不知道初始值的人,就很难看出生成的数值有什么规律。这就是伪随机的本质。
但是,这一切的前提是,你要给小学生一个随机的初始值。假如你每次都给他一个一样的值,他每次也都会计算出一样的答案(除非他算错了,当然这是很可能的事),这样就不随机了。可惜的是,rand()函数并不负责提供这个随机的初始值,它只负责采样,而这个初始值在没有人为设定的情况下每次都是一样的,这就导致每次运行程序生成的随机数都一样。
那么,假如我们想要一开始时提供一个随机的初始值(此处专业术语即“种子”),一个比较容易想到的方案是:用时间作为种子。<time>标准库提供了获取时间和时间计算的方法。其中,time(nullptr)获取的是从公元某某年开始到现在的秒数。
我们来做一个简单的实验:
#include <cstddef>
#include <ctime>
#include <ios>
#include <iostream>
int main(int argc, char *argv[]) {
std::cout << std::fixed;
while (true) {
double t = time(nullptr);
std::cout << t << std::endl;
bool state;
std::cin >> state;
if (state)
break;
}
return 0;
}
这段函数的作用是每次输出一下当前的秒数。因为cin是阻塞的,所以理论上每次输出的数值间隔取决于你输入的频率。
以下是某次输出的结果:
1768788441.000000
0
1768788443.000000
0
1768788445.000000
0
1768788449.000000
0
1768788450.000000
0
1768788451.000000
0
1768788454.000000
1
可以看到,time(nullptr)获取的时间本质上是一个整数,只能精确到秒。通过以上的输出,你其实可以推算出我运行这段程序时的绝对时间。
回归正题,我们需要生成一系列随机数,直接使用rand()函数无法实现每次都随机,直接使用time()函数更不是随机。但是假如我们用time()来作为随机数计算的“种子”,整个过程感官上就非常随机了。
实现方法是,在程序开始前使用srand(time(nullptr))来以当前时间作为种子,之后每次使用rand()函数,我们就可以实现随机数的获取了。
我们来做一个简单的掷骰子小游戏:
#include <cstdlib>
#include <ctime>
#include <iostream>
const int maxHealth = 3;
int throwADice() { return rand() % 6 + 1; }
int main(int argc, char *argv[]) {
std::srand(time(nullptr));
int currentHealth = maxHealth;
while (true) {
int answer = throwADice();
std::cout << "I throw a dice, guess the value of it:";
int assumption;
std::cin >> assumption;
if (assumption == answer) {
std::cout << "Damn! You get it!" << std::endl;
break;
} else if (abs(assumption - answer) <= 1) {
std::cout << "Almost figured out." << std::endl;
std::cout << "Current Health:"
<< (currentHealth >= maxHealth ? maxHealth : ++currentHealth)
<< std::endl;
} else {
std::cout << "You completely WRONG!!!" << std::endl;
std::cout << "Current Health:" << --currentHealth << std::endl;
}
if (currentHealth <= 0) {
std::cout << "You failed." << std::endl;
break;
}
}
return 0;
}
每回合会投一个六面骰子,假如你猜中了它的点数你就赢了,假如猜测的值和真实值只相差1,那么你会恢复一个生命值,否则你减一点生命值。
某次的输出结果:
I throw a dice, guess the value of it:3
Almost figured out.
Current Health:3
I throw a dice, guess the value of it:3
Almost figured out.
Current Health:3
I throw a dice, guess the value of it:3
You completely WRONG!!!
Current Health:2
I throw a dice, guess the value of it:3
You completely WRONG!!!
Current Health:1
I throw a dice, guess the value of it:3
You completely WRONG!!!
Current Health:0
You failed.
总之,考试会涉及的随机数生成方法大致就是如上了。但是从上面的分析过程中,你会发现这种原始的生成随机数的方法实际上有很多缺点,一方面它的计算算法简单导致随机数周期很短,另一方面在同一程序中你没办法“并发”的生成多个不同的随机数,因为所有随机数共用用一套种子。此外还有种种缺点,此处不再赘述。
如果想要更加现代的实现方式,我们需要使用C++的<random>库。但是我现在有点懒得写了。
template函数模板
这是一个非常强大的功能,可以让你的函数用同一套逻辑处理多种类型的数据。
一个简单的例子:假如你想要实现一个“加法”功能,返回两数之和,你可能会这么写:
int add(int a, int b){
return a + b;
}
但是这样写没办法用来计算double类型的数据,所以为了计算double类型的数据,你又写了一个同名的函数:
#include <iostream>
int add(int a, int b) { return a + b; }
double add(double a, double b) { return a + b; }
int main(int argc, char *argv[]) {
int x, y;
std::cin >> x >> y;
std::cout << add(x, y) << std::endl;
double m, n;
std::cin >> m >> n;
std::cout << add(m, n) << std::endl;
return 0;
}
这样,你就可以实现整数和整数相加、浮点数和浮点数相加。
但是“对于聪明的懒程序员”,既然这两个函数除了类型外完全一样,那我们为什么不写在一起呢?所以,我们完全可以这样写一个新的可以处理所有类型的add函数:
template<typename thisIsAType>
thisIsAType add(thisIsAType a, thisIsAType b){
return a + b;
}
之所以写thisIsAType意在说明这个地方写啥都行。实现的效果和写两个函数完全一致。需要注意的是,虽然后续你可以直接写add来表示两数相加,但是本质上经过了一个隐式的实例化过程。比如你想将两个整数相加,程序会先隐式转换为add<int>,之后再进行计算。也就是说,真正调用的是add<int>,add本身只是一个函数模版而非一个实际可以直接使用的函数。比如,对于两个int类型的变量a,b,你可以写add(a, b),但是你也可以显式实例化的写作add<int>(a, b),两者完全一致。
这里的typename表示这里是随便某个类型的代称。但是,这并不代表这里只能写typename,比如你可以这么写:
template <typename T, int N>
class Array {
T data[N];
};
使用方法:
Array<int, 10> arr;
这样你就可以创建一个长度为10、类型为int的自定义数据类型Array。template<int N>在这里表示输入数据为一个常量,所以他可以直接塞进数组后缀中。
template的能力远远不止于此。一个更加强大的功能是:它可以把一个函数塞进去。比如,此处我们来实现一个可以自定义排序规则的冒泡排序算法。
首先,我们先来写一个基础的冒泡排序算法:
#include <cstdlib>
#include <ctime>
#include <iomanip>
#include <iostream>
#include <utility>
#include <vector>
template <typename T>
void bubbleSort(std::vector<T> &targetVector) {
bool swapped = true;
for (int i = 0; i < targetVector.size() - 1 && swapped; i++) {
swapped = false;
for (int j = 0; j < targetVector.size() - 1 - i; j++) {
if (targetVector[j] > targetVector[j + 1]) {
std::swap(targetVector[j], targetVector[j + 1]);
swapped = true;
}
}
}
}
int throwADice() { return rand() % 6 + 1; }
int main(int argc, char *argv[]) {
std::srand(time(nullptr));
std::vector<int> test = {};
for (int i = 0; i < 10; i++) {
test.push_back(throwADice());
}
bubbleSort(test);
std::cout << std::left;
for (auto it : test) {
std::cout << std::setw(4) << it;
}
return 0;
}
这段代码综合了前面讲的随机数生成和后面会涉及的流运算符。总而言之,核心的逻辑就是bubbleSort函数,它会接受一个随便一个类型的vector,然后把里面的元素从小到大排列。这里我们还额外写了一个骰子函数,来生成测试数据。
某次的结果:
3 3 4 5 5 5 5 6 6 6
但是,我现在希望让它来按照与某个数的差的绝对值来从小到大排列,那么显然这样的代码就没办法正常工作了。我们当然可以重写bubbleSort函数,但是每次定义新的规则我们都要重写一遍的话实在是太麻烦了。
所以我们为什么不把函数直接传进去呢?我们可以定义一个比较函数,用来处理排序规则,返回值为false,则顺序保持不变;返回值为true,则需要交换顺序。
为了显示体现这样做的意义,我们修改骰子,使它变为一个"100面骰",同时,我们定义这样的一个比较函数,用来辅助排序:
template <typename T> bool cmp(T a, T b) {
if (abs(50 - a) < abs(50 - b))
return false;
return true;
}
当与目标(50)的绝对距离前者小于后者时,意味着两者无需调换顺序,否则需要调换顺序。
我们再来对bubbleSort函数进行调整,让它可以接受一个函数作为参数:
template <typename T, typename Func>
void bubbleSort(std::vector<T> &targetVector, Func cmpFunc) {
bool swapped = true;
for (int i = 0; i < targetVector.size() - 1 && swapped; i++) {
swapped = false;
for (int j = 0; j < targetVector.size() - 1 - i; j++) {
if (cmpFunc(targetVector[j], targetVector[j + 1])) {
std::swap(targetVector[j], targetVector[j + 1]);
swapped = true;
}
}
}
}
完整代码:
#include <cstdlib>
#include <ctime>
#include <iomanip>
#include <iostream>
#include <utility>
#include <vector>
template <typename T> bool cmp(T a, T b) {
if (abs(50 - a) < abs(50 - b))
return false;
return true;
}
template <typename T, typename Func>
void bubbleSort(std::vector<T> &targetVector, Func cmpFunc) {
bool swapped = true;
for (int i = 0; i < targetVector.size() - 1 && swapped; i++) {
swapped = false;
for (int j = 0; j < targetVector.size() - 1 - i; j++) {
if (cmpFunc(targetVector[j], targetVector[j + 1])) {
std::swap(targetVector[j], targetVector[j + 1]);
swapped = true; //直接比较大小改为了调用比较函数。
}
}
}
}
int throwADice() { return rand() % 100 + 1; }
int main(int argc, char *argv[]) {
std::srand(time(nullptr));
std::vector<int> test = {};
for (int i = 0; i < 10; i++) {
test.push_back(throwADice());
}
bubbleSort(test, cmp<int>) //注意这个地方需要显式实例化!
std::cout << std::left;
for (auto it : test) {
std::cout << std::setw(4) << it;
}
return 0;
}
某次的运行结果:
51 48 52 34 76 22 80 86 93 96
随机抽取的10个数按照和50的绝对距离从小到大排列。
通常来说,函数模版需要直接完整的写在头文件里。如果你硬要做原型和实现的分离,编译器会直接让你飞起来。
iomanip库
<iomanip>库是一个用来控制输入输出格式的头文件,它提供的是一组I/O操作符,即插入在输入输出流中的格式指令。
需要注意的是,流式运算符有两类格式控制,一种是修改流状态的操作符,而另一种是修改下一次输出的操作符。
简单理解来说,cout是一个“流对象”,但是它的实例化过程是在程序尚未开始运行前就在标准库中完成的。这个流对象有很多的状态来描述它的输出格式,比如输出的数字精度,比如输出的宽度以及向哪一侧对齐。在整个程序的生命周期中,cout只在程序开始之前被实例化,程序结束后被析构。
setw
在<iomanip>中,只修改下一次输出的状态符几乎只有一个:setw()。它会控制下一次输出的“宽度”,输出结束后这个宽度会自动复位为0。
我们来举个简单的例子说明此事:
#include <iomanip>
#include <iostream>
const int test = 12345;
int main(int argc, char *argv[]) {
for (int i = 0; i <= 10; i++) {
std::cout << test << std::setw(i) << test << std::endl;
}
return 0;
}
猜猜这段代码会输出什么?
答案揭晓:
1234512345
1234512345
1234512345
1234512345
1234512345
1234512345
12345 12345
12345 12345
12345 12345
12345 12345
12345 12345
每一次输出都有一个隐藏的“输出宽度”,当本次输出的文本长度大于宽度时,下一次输出就会直接接在后面;如果文本长度小于宽度,下一次输出就会先补全所要求的宽度,再接上下一次的输出。默认的输出宽度为0,意味着默认情况下哪怕你只输出一个字符,下一次的输出也会直接接在后面。
流状态操作符
因为除了setw的所有流式操作符都直接修改cout的全局状态,所以你完全可以不必每次输出时都设置一遍。比如,你可以这么写:
#include <iomanip>
#include <ios>
#include <iostream>
const double pi = 123.456789;
int main(int argc, char *argv[]) {
std::cout << std::setprecision(4);
std::cout << pi << std::endl;
std::cout << std::fixed;
std::cout << pi << std::endl;
std::cout << std::setprecision(6);
std::cout << pi << std::endl;
std::cout << std::scientific;
std::cout << pi << std::endl;
return 0;
}
输出结果为:
123.5
123.4568
123.456789
1.234568e+02
其实说到底,对于像cout这样的流对象,使用<<来写入内容时把所有东西写在一个std::cout«…中和每行写一个cout没有任何区别。比如上面的这段代码你也完全可以这么写:
#include <iomanip>
#include <ios>
#include <iostream>
const double pi = 123.456789;
int main(int argc, char *argv[]) {
std::cout << std::setprecision(4) << pi << std::endl
<< std::fixed << pi << std::endl
<< std::setprecision(6) << pi << std::endl
<< std::scientific << pi << std::endl;
return 0;
}
全部塞在一个cout里,结果完全一致。
以下罗列一些常用的<iomanip>函数:
setprecision(n)设置输出的有效位数fixed/scientific设置有效位数的模式,fixed表示小数点后若干位为有效位数,scientific表示使用科学技术法表示有效位数。left/right表示对齐的方式。在一个输出宽度内,你的文本可以是左对齐,也可以是右对齐。setfill(ch)设置一个输出宽度内空白部分的填充字符。默认啥也没有。showpoint强制显示小数点dec/oct/hex显示十进制、八进制、十六进制。
我们来举个经典例子:九九乘法表。
#include <iomanip>
#include <iostream>
#include <string>
#include <vector>
template <typename T> struct Vector2D {
T x;
T y;
std::string content;
bool state;
};
Vector2D<int> tableMap(Vector2D<int> inputVector) {
return Vector2D<int>{inputVector.y, inputVector.x, inputVector.content,
inputVector.x >= inputVector.y};
}
template <typename Func>
void tablePrinter(std::vector<int> vec01, std::vector<int> vec02,
Func tableFunc) {
std::cout << std::left;
std::vector<std::vector<std::string>> table(
vec01.size(), std::vector<std::string>(vec02.size()));
for (int i = 0; i < vec01.size(); i++) {
for (int j = 0; j < vec02.size(); j++) {
Vector2D<int> inputVector = {i, j,
std::to_string(vec01[i]) + '*' +
std::to_string(vec02[j]) + '=' +
std::to_string(vec01[i] * vec02[j]),
true};
Vector2D<int> outputVec = tableFunc(inputVector);
table[outputVec.x][outputVec.y] =
outputVec.state ? outputVec.content : " ";
}
}
for (auto it : table) {
for (auto unit : it) {
std::cout << std::setw(10) << unit;
}
std::cout << std::endl;
}
}
int main(int argc, char *argv[]) {
std::vector<int> numbles = {1, 2, 3, 4, 5, 6, 7, 8, 9};
tablePrinter(numbles, numbles, tableMap);
return 0;
}
输出结果:
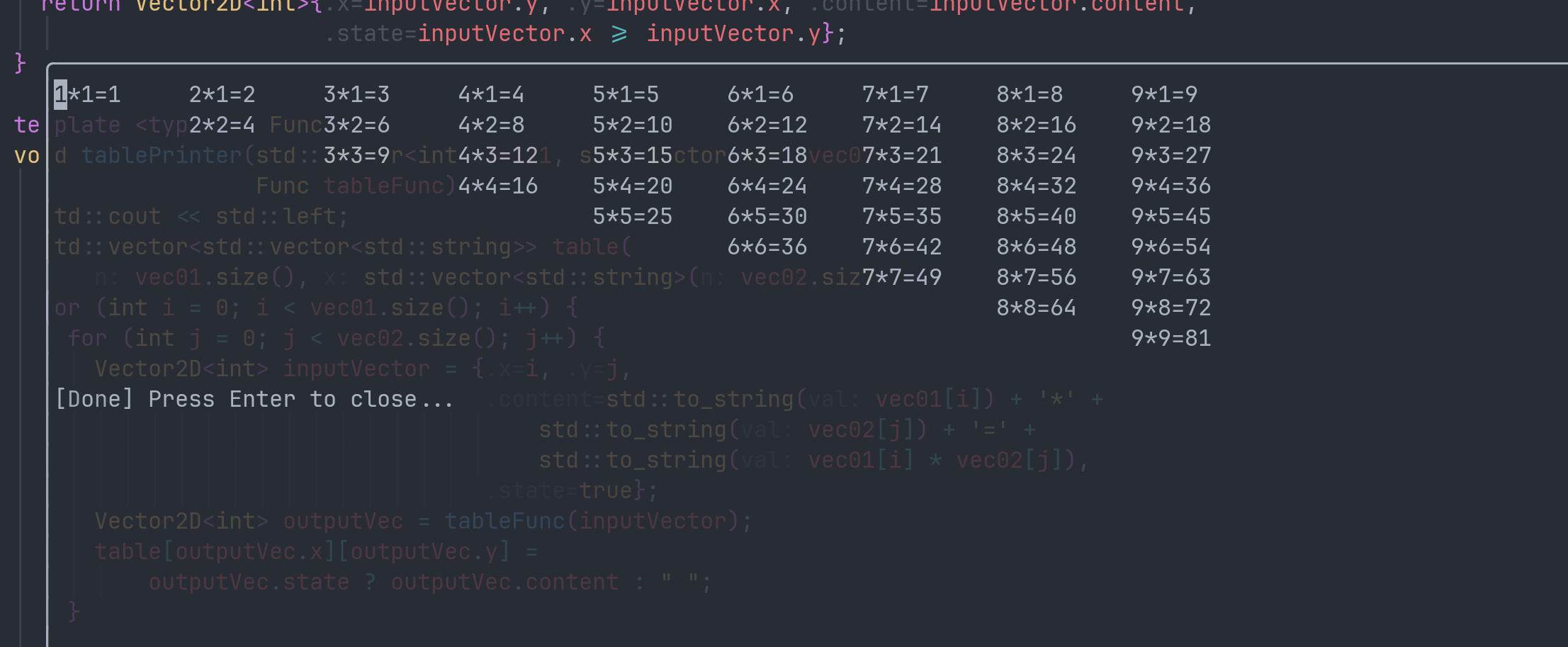
你可能注意到了,这段代码中tablePrinter函数接受了一个映射函数。这意味着我们可以通过修改映射规则的方式调整打印格式。通过这样的写法,我们可以快速的写出所有方位角度的乘法表,甚至可以整出一些花活。
#include <iomanip>
#include <iostream>
#include <string>
#include <vector>
template <typename T> struct Vector2D {
T x;
T y;
std::string content;
bool state;
};
Vector2D<int> Leftdown(Vector2D<int> inputVector) {
return Vector2D<int>{inputVector.y, inputVector.x, inputVector.content,
inputVector.y >= inputVector.x};
}
Vector2D<int> LeftUp(Vector2D<int> inputVector) {
return Vector2D<int>{8 - inputVector.y, inputVector.x, inputVector.content,
inputVector.y >= inputVector.x};
}
Vector2D<int> RightDown(Vector2D<int> inputVector) {
return Vector2D<int>{inputVector.y, 8 - inputVector.x, inputVector.content,
inputVector.y >= inputVector.x};
}
Vector2D<int> RightUp(Vector2D<int> inputVector) {
return Vector2D<int>{8 - inputVector.y, 8 - inputVector.x,
inputVector.content, inputVector.y >= inputVector.x};
}
template <typename Func>
void tablePrinter(std::vector<int> vec01, std::vector<int> vec02,
Func tableFunc) {
std::cout << std::left << '\n';
std::vector<std::vector<std::string>> table(
vec01.size(), std::vector<std::string>(vec02.size(), " "));
for (int i = 0; i < vec01.size(); i++) {
for (int j = 0; j < vec02.size(); j++) {
Vector2D<int> inputVector = {i, j,
std::to_string(vec01[i]) + '*' +
std::to_string(vec02[j]) + '=' +
std::to_string(vec01[i] * vec02[j]),
true};
Vector2D<int> outputVec = tableFunc(inputVector);
table[outputVec.x][outputVec.y] =
outputVec.state ? outputVec.content : " ";
}
}
for (auto it : table) {
for (auto unit : it) {
std::cout << std::setw(10) << unit;
}
std::cout << std::endl;
}
}
int main(int argc, char *argv[]) {
std::vector<int> numbles = {1, 2, 3, 4, 5, 6, 7, 8, 9};
tablePrinter(numbles, numbles, Leftdown);
tablePrinter(numbles, numbles, LeftUp);
tablePrinter(numbles, numbles, RightDown);
tablePrinter(numbles, numbles, RightUp);
return 0;
}